Amona ez zait ba etorri laguntza eske!
Bere 19 bilobei oparitxo bat egin nahi die eta 19 harritxo (txikiak, oso txikiak) jarri dizkit mahai gainean. Berak margotu ditu eta oso koloretsu gainera. Eta kontraste handiz biloba bakoitzaren izen-abizenen lehen hizkiak idatzi ditu harritxo bakoitzean.
Eta zertan lagundu dezaket nik, bada?
Hantxe jarri dit, harritxo guztien ondoan paper orri handi handi handi bat. A0 tamainakoa hain zuzen ere! Bere eskaera da ahalik eta paper gutxiena xahutuz eta tamaina estandarreko paper orriak itzuliz, harritxo bakoitzarentzako poltsatxo bat egin dezadan.
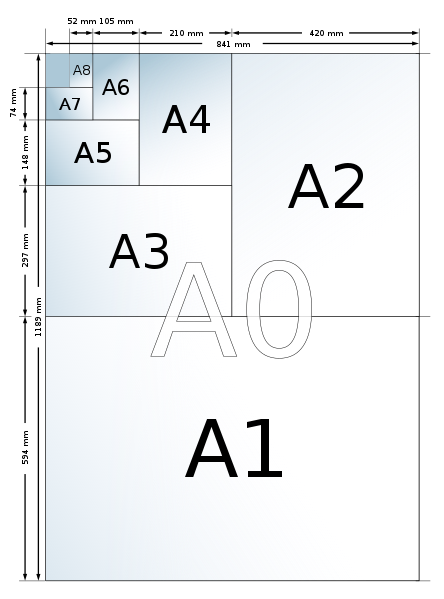
Neurtzeko zinta hartu eta kalkulu batzuk egin ondoren ohartu naiz harritxo bakoitzeko A8 neurriko paper txiki batekin nahikoa izango dudala. Kontuan izan A0tik A1era basatzeko papera erdibitu egin behar dela eta berriro erdibitu A1etik A2ra pasatzeko. Horrela, erdibitzen jarraituz gero, A8 tamainara irits gaitezkeelarik. Irudian ikusten den bezala:
Beraz, artaziak edo guraizeak hartu eta papera erditik mozten hasi naiz, ahal den neurrian paper ahalik eta handienak utziz.
Ea orain zuek niri laguntzen didazuen. Amonari neurri estandarreko ahalik eta paper orri handienak itzuli nahi badizkiot, neurri bakoitzeko zenbat itzuliko dizkiot 19 harritxoak bildu eta gero?
Gogoratu! https://guaixe.eus/komunitatea/EdurneLarraza helbidean aurkituko duzue ekarpen hau eta bertan zuen erantzunak emateko aukera izango duzue. Nola lortu duzue erantzuna? Gainera, astebete barru nire azalpenak emango dizkizuet. (www.bebras.uk webgunetik ekarria).ERANTZUNA (2020/03/13an gehituta):
Ekarpen honetan adierazpide bitarrarekin jarraitzen dugu, baina oraingoan beste ikuspuntu batetik begiratu. Izan ere aurretik esana dugu bitarra sistema posizionala dela, hamartarra bezala. Horrek esan nahi du posizio bakoitzeko zenbakiak posizio horretako pisuarekin biderkatu egiten direla. Hau da, hamartarrez 0. posizioan digitua x 1 (batekoak), 1. posizioan digitua x 10 (hamarrekoak), 2. posizioan digitua x 100 (ehunekoak), eta abar, biderkatzailea 10en berredurak izanik.
Bitarrez ordea x1, x2, x4, x8, x16, x32, eta abar egiten da, oraingoan biderkatzaileak 2ren berredurak izanik.
Ondo konturatzen bagara paperen neurrietan ere ezaugarri hau ematen da. A7a A8aren bikoitza da eta A6a A7aren bikoitza, hau da, aldiro 2ren berredura inkrementatzen ari gara. Beraz, A4 batekin A8 neurriko 16 zorro egin ahal izango ditugu, A7 bat beharko dugu beste bi zorro egiteko eta azkenik A8 bat gehiago. Horrela 19 A8 neurriko zorro izango ditugu. Eta galderari erantzuteko, zein neurritako paperak itzuliko ditugu?
Bada, A0a bitan zatitu dugu. Horrela A1 neurriko paper bat geratuko zaigu eta bestea jarrituko dugu zatitzen. A1 hori zatitzea 2 A2 lortuko ditugu. A2 bat gorde eta bestea zatitu. Zatitzen dugu A2tik 2 A3 lortuko ditugu. A3 bat gorde eta bestea zatitu 2 A4 lortuz. A4 bat erabiliko dugu 16 zorro egiteko eta bestea zatitzen jarraituko dugu 2 A5 lortuz. A5 bat gordeko dugu eta bestea zatitu 2 A6 lortuz. A6 bat gorde eta bestea zatitu 2 A7 lortuz. A7 batetatik 2 zorro egingo ditugu eta bestetik beste 2 A8 lortuko ditugu. A8 bat gorde eta bestearekin 19. zorroa lortuko dugu.
Erantzuna beraz: A1, A2, A3, A5, A6 eta A8 tamainako paper banarekin geratuko gara.
Bitarraren izaera hau asko erabiltzen da konputazioan. Adibidez bilaketa algoritmoetan.
Ongi segi!
